Day 76: CLT not BLT!

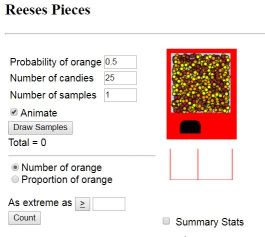
Today we revisited the Rossman/Chance Reeses Pieces Simulation to look at once again the sampling distribution of proportions.  Using this simulation, we reviewed notation, which is so challenging for students when they first see it.

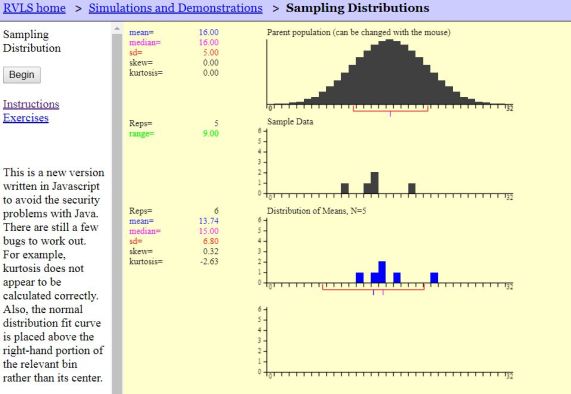
We then used the Rice Virtual Labs to set the groundwork for the assumptions and conditions of a sampling distribution of means and the two situations for knowing it is approximately Normal: Normal population vs. unknown population.

My AP Stats students, using their iPads, explored what happens when the population is Normal, when it is not, and whether they could come up with a population that would not yield an approximately Normal sampling distribution.  Once again, we reviewed the notation and also determined the formula for the standard deviation…they actually came up with the rule!!

Love having technology at my students’ finger tips!  And thanks to Rossman/Chance for updating the applets to work with iPads…so much better when students do their own exploring rather than watching me do it at the front.

Day 75: SINning in Stats

Today we begin the journey to Inferential Statistics in my AP Statistics class.  And I use the development of the sampling distribution of a statistic as a means to set up good habits as well as develop the conceptual understanding of why we need to check conditions for the elements of the sampling distribution: Center, Spread, and Shape.

I found that students really struggled with all of the apparently different conditions for the various inference methods we study in second semester.  I really wanted to streamline the process of checking the conditions. After looking at and comparing the various assumptions and conditions, I realized that the two sampling distributions used in the inference procedures about proportions or means boiled down to two things: a random element in the data collection method (simple random sample or randomized experiment), and sample size where one needs both a large enough and a small enough sample to determine the standard deviation and shape.  In addition, I needed to help my students understand the difference between assumptions and conditions.

Here is a summary of what I found:

Assumptions:

Independence Assumption: The sampled values must be independent of each other

The Sample Size Assumption: The sample size, n, must be large enough

Assumptions are hard—often impossible—to check.  Still, we need to check whether the assumptions are reasonable by checking conditions that provide information about the assumptions.  The corresponding conditions to check before using the Normal to model the distribution of sample proportions or means are the Randomization Condition, 10% Condition and the Success-Failure Condition/Large Enough Sample Size Condition.

Conditions you can check:

Randomization Condition: The data must be representative of the population. (That is, it must come from a randomized experiment, or from a simple random sample of the population; the sampling method must be unbiased.)

10% Condition: The sample size, n, must be no larger than 10% of the population.

Success/Failure Condition: The sample size must be large enough so that we can expect at least 10 “successes” and 10 “failures”. That is, np > 10  and nq > 10  OR  Large Enough Sample Condition: If the population is unimodal and symmetric, any size sample is sufficient. Otherwise, a larger sample is needed.

I also wanted it have some kind of cognitive framework to fit these ideas.  How could I combine the ideas into chunks that include the essence of the assumptions and conditions?  Well, Random made its own sense, but Independence and the 10% condition were intertwined, and the approximately Normal shape was tied to having a large enough size sample via success vs fails or simply a larger sample was better.

Acronyms are great memory devices, especially when first learning about something new and complex.  The acronym is a simple organizational tool that reminds the user of the complex ideas.  My next thought was what kind of acronym could I come up with for these?  RIN (for random, independence and normal)..but there was no real hook or interesting connection with RIN.  How about SIN where S stood for random Sample…but that was somewhat suspect because not all inference is about sampling, so I did stretch it a little to say SRS or random assignment (they both sound essy).   And I use the catchy phrase, “It is a SIN to not check the conditions.”  And I have found that my kiddos don’t forget to check them….phewww!

Here is an example of how we talk through these ever important assumptions and conditions.  As the year progresses, we fine-tune and focus in on the important distinctions, but the acronym SIN and these three words give us a simple framework to talk about the distinctions.  To set the groundwork for next semester, I have students recognize the assumptions/conditions AND what the condition guarantees.

 

Day 91: Fresh Start

We are starting the new semester today, as many schools around the country are.  The kids seem relaxed and ready to go after their finals experience.  In AP Statistics, I didn’t have time to assess on Sampling Distributions, so the students agreed to put off the exam until after finals…great to have student voice in some decision making (also gave me time to write the assessment – haha).  So today we reviewed the key similarities and differences in sampling distributions for proportions and means via a graphic organizer.  I thought about making a foldable to fit the information, but I wasn’t sure I’d get the biggest bang for my time, since classes were only 30 minutes long on this first day.  So we wrote it out together and it seemed it went well.  I even had a student say that “it finally clicked!”  Fresh starts and rested minds are something to behold!

I am also thrilled that I have been keeping up with the premise of the blog 180 idea.  Some days I get behind, but I usually use the week-end to catch up.  Of course the end of the semester caught me, so I have some back-filling to do.  I love the documentation, but I haven’t used the blog as a consistent reflection tool.  Typing out all of my thoughts tends to take me a long time, as writing isn’t my strength.  I did get Dragon, a speech-recognition software by Nuance. for Christmas, and I’m really excited to try it out.  I believe talking out my thoughts rather than typing might result in some deeper reflection.  But I haven’t installed it yet as we may be getting new school computers and I don’t want to waste my software license.

 

Day 85: Sampling Distribution Rubric

 

One of the most challenging aspects of AP Statistics is the technical writing required.  Students are not used to writing in supporting details and following a prescribed format.  Although I give them an acronym to help them through the steps, their writing often lacks detail and critical components.

I use the 4-step process (Think, Plan, Do, Conclude) as a scaffold for students to organize their writing in inference procedures.  I also don’t like to hit them with “everything” all at once when we begin the inference units.  So I have used the Sampling Distribution unit to incorporate the 4-step process along with many of the components of inference procedure requirements.  Most importantly, I “enforce” the use of the probability statement: P( statistic > value) idea, introduce the conditions for building the sampling distribution (which are soooooo similar to those in inference procedures) and writing conclusions in context.  I have found this to be extremely helpful since students then already know the procedure and all we do is “tweak” it during inference.

As part of my professional evaluation process, I decided I wanted to try to quantify and rubricize (I don’t think that’s a word..haha) the process so I would have quantifiable data.  I matched the 4-step process with the essential AP requirements associated with each step.  Wanting to have 4 components under each step of the 4-step process, I went through the comments of the head grader of previous AP exams to look for insight into the components of each step. I looked for ways to connect inference language to sampling distribution language.  I also wanted the rubric to use the grading process of an AP free response question (E, P, I) as well as the overall grading score (4-1).  Unlike the AP grading, I am demanding more for what qualifies as an E, P and I; students must have all 4 components of a step to get an E and they must get all 4 step at an E to get a 4 for the problem.

I hope this guides my students to a well-written response while encouraging them to pay attention to details…the killer on the AP exam.  I will use this rubric often with students in a formative assessment way, encouraging student reflection on their writing.  I am excited that the Common Core seems to be requiring more thoughtful student responses with supporting details and proper use of vocabulary.  How do you create rubrics for student learning?

Day 81: Population, Sample, Sampling Distribution, Oh My!

The whole idea of a Sampling Distribution is mind-blowing for first time statistics students.  Part of the problem is vocabulary, part is the notation, and part is the concept of the mean of the means or mean of the proportions.  Lots of layers of complexity.

 

I must say that the Rice University applet on Sampling Distributions is just awesome!  I’ve used this applet for years now and I have not found a more versatile, yet easily accessible, visual. Students get a concrete, visual introduction to the concepts surrounding the building of a sampling distribution…and it works now on our iPads.  Yay!! Give it a try…I think you’ll fall in love with it, too.  What visual aids do you use in the classroom to help students get a mental picture?

Day 79: Awesome Statistics Applets

Can I say that I “heart” the Rossman/Chance Applets even more this year!  Many of the applets have been updated to java script (js), which means my kiddos can now access them on their iPads.  Because I had to run the simulation at the front of the board, my students could “space out” on the sense-making, observing, analyzing and reasoning that I want them to do.  I so missed having them individually explore the concepts around sampling distributions, and now they can!  THANK YOU!

Using the Reeses Pieces applet as an introduction to the concepts of sampling distributions is uber-fun…well, at least for me it is and I do think the kids appreciate the effort to have a variety of activities to develop and deepen their understanding.

And here is the summary of their observations, with my help to connect the “conditions” to develop the sampling distribution of sample proportions.