Day 101: Logs in Life Peer Review

My precalculus students completed a project on logs and logistics function in real world.  Before break, they signed up for a topic where logs or logistic functions are used. Students signed up for two possible topics and referenced them with an online site, which they submitted through a Google Form. Since Google Forms are time stamped, I able to use a first come, first served approach to topic assignment. I allowed up to 3 people to select the same topic, but after that, they got their second choice. Out of two classes, I only had 4 students that needed to determine a new topic.

Here is a brief synopsis of what was required:

THE TASK: The end product of your webquest will be a BROCHURE describing what you have learned about your chosen application of logarithms. • Brochure style (tri-folded) • Typed in your own words • Description and history of the application (e.g. “what is a decibel?” and “who invented the Richter scale?”) • Description of mathematics used in calculations – specifically logarithms with an example • Description of at least one career in which this application is used • At least one relevant graphic Citation of other websites used beyond the ones given (just list the url)

Students submitted both a physical copy and an electronic one.  I created groups of brochures with different topics and none created by a particular group member.

Today they did the peer review of the brochures, again using a Google Form.  I used radial buttons for the rubric part of the assessment. There was also a required comment section. I asked students to give both a positive comment about an intellectual aspect of the topic presentation and a constructive criticism. Part of their grade is their review of their peers and their peers’ review of their pamphlet.  You could have heard a pin drop.

 

We had 10 minutes left in class, so I tried something on the fly…never know how that will go. I asked the groups to discuss and determine the most interesting brochure. They then passed that one on to the next group.  Maybe this will be part of the whole process next year.

Day 94: Class Discourse Sparked by Navigator Quick Poll

One of the things I’d like to use more often in my Precalculus classes are multiple choice questions to promote class discussion.  Today as part of the opener I gave my first MC question.  Fairly straight forward question because I wanted to get the kiddos logged into the Nspire Navigator, which we haven’t done for a while.  The students wrote down on their Opener-Exit slip the answer along with any calculations they needed to do to determine the best choice. Then the Navigator, through a Quick Poll, collects their answers. Once I stop the poll,  I can project the responses in a bar chart.

As you can see, there were two popular answers.  I asked my students in their groups to discuss their choices and try to determine which one was actually the correct answer along with supplying a reasoned argument for their group’s choice.  Some great conversations!  I then resent the Quick Poll to see if they could arrive at the correct answer without my confirming the answer.

Day 85: Polar Equations Finished!

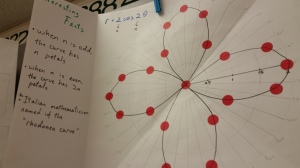
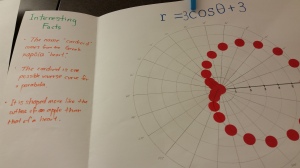
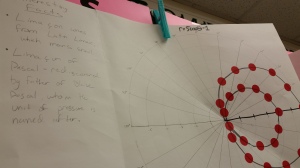
They are done!  The polar equation graphs my precalc students started on Friday are finished…in fact they came into class asking if they could have time to finish ‘cuz they really wanted to see the final results.  I like the component of finding the name of their equation type as well as researching then sharing least 2-3 interesting facts about their polar equation.

Day 84: Hands on Polar Equations

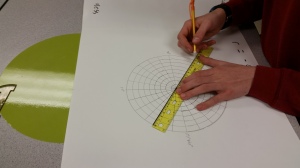
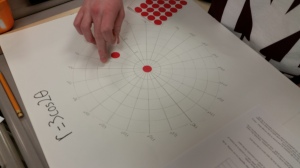
Many years ago (I don’t want to say how many but it was before we had access to graphing calculators), I had my students hand draw various polar equations.  Having technology so readily available now, this project had been shelved and collecting dust. I decided today that I wanted my precalculus students do experience a tactile activity today.  Although I love polar equations, it just didn’t fit the timeline this semester (maybe we’ll revisit next semester).  But why not give them an initial exposure to Polar Equations and their graphs as a way to review polar coordinates just before finals…and besides, the graphs are fun and unexpected.

I wrote up the activity and made some decisions about how to have students make posters.  A few years ago our department invested in large boxes of poster paper (you can see the poster paper in many of my posts) which was a pretty cheap investment for the amount of paper…and the box seems to last for a couple of years at least.  I wanted the paper to be a square in order to find the center and create the polar graph paper.  Once I folded to create the square, I thought, why not use the flap for added info.  Here is my prototype that I had posted on the front white board.

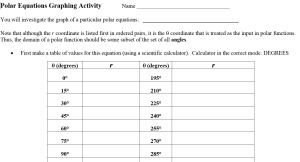
I then wrote up the directions, including a chart for my students to record the r-values for their equation. I did not tell them the names of the graphs, just handed out various equations; each student got a unique one. I was ambitious with what I wanted them to do afterwards (and we didn’t get that far), but I would keep the “interesting facts” part of the activity.

Then I handed out the directions and away they went.  I had hoped they would finish in the class period, but some of my students are very meticulous so it took a while for them to create the polar graph paper on the poster.  I am still pondering how to improve that aspect of the activity.  Anyway, here are some photos of the activity in progress:

 

  

Hopefully they will finish on Monday.  Happy Week-end

Day 80: Folder Trig

One activity I started last year to get students thinking about constraints and possibilities of an application problem is what I call the “Folder Activity.”  This time around, I wanted my students to be thinking about what makes a problem sinusoidal and what information from the situation helps to create a mathematical model (equation).  In addition, I want them to be thinking about what kinds of questions could be asked about the situation that can be answered with the graph and/or the function equation.

To set up this activity, I needed lots of sinusoidal application situations that are different from the typical situations of ferris wheels, merry-go-rounds and oscillating springs.  The internet is a great source for these and I found many!  I then “pull apart” the problem situation from the questions asked.  The students only get the problem situation…here is one example of the eight different problems I had available:

 

First of all, students open the task card on their iPad.  This includes group roles, materials needed, the task and the product.  Here is a copy of the tasks and folder layout.

 

The groups then get a folder, a quarter sheet headed with “Known Information,” a second quarter sheet headed with “Mathematical Relationships,” and a half sheet of graph paper.  At this point they read and discuss the problem information, determine known information and identify potential useful mathematical relationships…they know not all of the possible mathematical relationships will be used, but it is helpful to think about them.  The discussions are rich, the misconceptions get “fixed” most of the time, and once the questions are actually asked, they already have a plan to answer them.

     

Once the information is organized and glued to the folder, then the group can pick up the actual questions and begin working on them.

 

The final product is the folder with the solution written out neatly…each person’s handwriting needs to be apparent in the solution write-up.  All is glued in the proper places and finally the group evaluates to what extent they used the 8 Math Practices along with a 1-2 sentence summary for each practice.

 

Day 78: Not All Mistakes are Bad, IF You Learn From Them!

I’ve been reading the book, Total Participation Techniques: Making Every Student an Active Learner by Persida Himmele and William Himmele, published by ASCD (can also be found online and downloaded if you are a member of ASCD).  The authors talk about getting your students actively engaged AND cognitively invested in the learning rather than being “listening objects” in the classroom.  One quote that resonated with me was:

At any age, people need to pause and process what they are learning. They need to chew on concepts, jot down their thoughts, compare understandings with peers, and articulate their questions…and celebrate the learning that is happening right now in my head.

As a follow-up to solving trig equations, I had my students create posters, but I wanted them to do more.  I found a great idea from Rebecca Peterson called the Mistakes Game.  I adjusted the directions some and came up with this activity:

The Tasks:

SOLVE CORRECTLY:

1. As a group, work your given problem correctly.  Then, check your answer using graphing technology.
2. Once you have the correct answer(s), write out the solution process neatly on a poster paper.
3. Include a graph of the original function and the location of the solutions (color-code by principle solution and symmetry solution.)

INTRODUCE A COMMON MISTAKE:

4. Now work the problem incorrectly, hiding your mistake as cleverly as possible.  Your “mistake” must be a true pitfall of the given problem (i.e., what kinds of conceptual errors would students likely make?).  Your error cannot be a simple arithmetic or algebraic mistake unless it is related to using an Algebra Trick incorrectly.
5. When you’re happy with your “lie”, put it on the back of your poster paper. Post this side for all to see.

FIND THE ERRORS:

6. When every group is done, you will find the errors on the other posters and vote on the group with the sneakiest mistake.
7. Be prepared to discuss/defend your results.

I really like the idea of coming up with a mistake.  This causes the students to use higher-order thinking skills to analyze and synthesize.  This is cognitive engagement at its best.  I heard lots of discussion around the process, with students correcting others and helping them understand their error; but then the magic happened!  Trying to think of a mistake one could make when solving a trig problem, and the idea that they need theirs to be “tricky” led them to go through many of the common errors.  They were talking about what would be an error and by deciding if it was “tricky” enough, they had to understand the nature of the error.  I am really excited to see if this process helps students to think more carefully while they solve trig equations and to avoid those common pitfalls.

Day 77: Multiple Representations for Trig Equations

In precalculus, we have begun to look at solving trigonometric equations.  Yesterday, we developed the general rules for finding solutions for the Big Three trig functions: sin^-1x + 2πn, π – sin^-1x + 2πn,  cos^-1x + 2πn, 0 – cos^-1x + 2πn, and  tan^-1x + πn

I am a bit of a stickler as I require students to use the inverse trig function definitions correctly while solving equations.  As an opener, students were asked to do the following:

Find all solutions for the equation: sin2x = – ½.  Now find the particular solutions in the domain: [1,5].  Verify solutions graphically.

My goal for this problem was to connect the algebraic process of solving the equation to the graphical results; that is, I wanted multiple representations and understanding for what was really happening..  Once again I wanted the conceptual underpinning to be solid as my kiddos practiced equation solving procedures; that is, I didn’t want mindless robots solving equations without thinking about what was really happening.

I also got to use my Mathematical Practices labels!  Double score.

Day 74: Snowflake Lane – Trig Style

As one of the Trig Review Stations, student had to graph a trig function alone with it’s reciprocal function.  How boring in and of itself…so decided to have them glue the graph on one side of a pre-cut snowflake (found at Michaels on sale for 99¢) and the initial equation on the other side.  Students used a green pen to graph the initial function and a red pen to graph its reciprocal.  Nice discussions as my students completed the task, particularly one who remarked that this helped him clarify inverse with reciprocal…yay!!

 

Aren’t these fun and also decorates my room for wintertime….notice, no snow yet.  What are ways that you have used a skill practice experience to do double duty as room decoration?

Day 73: Big Trig Assessment Day!

Well, here we are!  Today’s the day for my kiddos to shine.  Although few students popped in this morning for last minute help (that’s a good thing, right?) they seemed a little nervous at the start of the period, so I offered them a smile and a pat on the back at any time during the exam….some took me up on it at the end of the test…so made me smile!!

I wish I was more organized outside of school so that I would bake some pi sugar cookies (I think I have a pi-cookie cutter somewhere).  What do you do to help your students relax prior to and during an assessment?

Day 72: Reviewing for the Big Trig Assessment

We are finally at the end of the introduction to trigonometry in precalculus…and to have an assessment that covers the breadth of the topics, my teaching partner and I decided we would create a two-day assessment, one day being non-calculator part and the other day being a calculator part; so each day is written as a class period assessment.  In order to get ready, my students were given a review sheet, but in class, having me drone on about the topics and going over problems can be deadly.  So….we created 8 Trig Stations (see the post from last year to get some more details) that cover the 8 big topics.  Students are in groups of 3-4 and have 10 minutes to work at each station…even if they don’t finish, they move on.  This year, students requested to take photos of the questions if they didn’t finish along with the answers (found in the orange envelopes).

Most students found the experience helpful for identifying the areas they needed to focus on for studying.  This year I even taped some of the conversations (unbeknownst to the group) so I could hear them use some of the mathematical practices including Sense-make, Reason, Argument, Model, Tools, Precision of language use, and Structure.  They were very enlightening and encouraging!

What do you do to check on student use of the math practices?