Day 80: Folder Trig

One activity I started last year to get students thinking about constraints and possibilities of an application problem is what I call the “Folder Activity.”  This time around, I wanted my students to be thinking about what makes a problem sinusoidal and what information from the situation helps to create a mathematical model (equation).  In addition, I want them to be thinking about what kinds of questions could be asked about the situation that can be answered with the graph and/or the function equation.

To set up this activity, I needed lots of sinusoidal application situations that are different from the typical situations of ferris wheels, merry-go-rounds and oscillating springs.  The internet is a great source for these and I found many!  I then “pull apart” the problem situation from the questions asked.  The students only get the problem situation…here is one example of the eight different problems I had available:

 

First of all, students open the task card on their iPad.  This includes group roles, materials needed, the task and the product.  Here is a copy of the tasks and folder layout.

 

The groups then get a folder, a quarter sheet headed with “Known Information,” a second quarter sheet headed with “Mathematical Relationships,” and a half sheet of graph paper.  At this point they read and discuss the problem information, determine known information and identify potential useful mathematical relationships…they know not all of the possible mathematical relationships will be used, but it is helpful to think about them.  The discussions are rich, the misconceptions get “fixed” most of the time, and once the questions are actually asked, they already have a plan to answer them.

     

Once the information is organized and glued to the folder, then the group can pick up the actual questions and begin working on them.

 

The final product is the folder with the solution written out neatly…each person’s handwriting needs to be apparent in the solution write-up.  All is glued in the proper places and finally the group evaluates to what extent they used the 8 Math Practices along with a 1-2 sentence summary for each practice.

 

Day 78: Not All Mistakes are Bad, IF You Learn From Them!

I’ve been reading the book, Total Participation Techniques: Making Every Student an Active Learner by Persida Himmele and William Himmele, published by ASCD (can also be found online and downloaded if you are a member of ASCD).  The authors talk about getting your students actively engaged AND cognitively invested in the learning rather than being “listening objects” in the classroom.  One quote that resonated with me was:

At any age, people need to pause and process what they are learning. They need to chew on concepts, jot down their thoughts, compare understandings with peers, and articulate their questions…and celebrate the learning that is happening right now in my head.

As a follow-up to solving trig equations, I had my students create posters, but I wanted them to do more.  I found a great idea from Rebecca Peterson called the Mistakes Game.  I adjusted the directions some and came up with this activity:

The Tasks:

SOLVE CORRECTLY:

1. As a group, work your given problem correctly.  Then, check your answer using graphing technology.
2. Once you have the correct answer(s), write out the solution process neatly on a poster paper.
3. Include a graph of the original function and the location of the solutions (color-code by principle solution and symmetry solution.)

INTRODUCE A COMMON MISTAKE:

4. Now work the problem incorrectly, hiding your mistake as cleverly as possible.  Your “mistake” must be a true pitfall of the given problem (i.e., what kinds of conceptual errors would students likely make?).  Your error cannot be a simple arithmetic or algebraic mistake unless it is related to using an Algebra Trick incorrectly.
5. When you’re happy with your “lie”, put it on the back of your poster paper. Post this side for all to see.

FIND THE ERRORS:

6. When every group is done, you will find the errors on the other posters and vote on the group with the sneakiest mistake.
7. Be prepared to discuss/defend your results.

I really like the idea of coming up with a mistake.  This causes the students to use higher-order thinking skills to analyze and synthesize.  This is cognitive engagement at its best.  I heard lots of discussion around the process, with students correcting others and helping them understand their error; but then the magic happened!  Trying to think of a mistake one could make when solving a trig problem, and the idea that they need theirs to be “tricky” led them to go through many of the common errors.  They were talking about what would be an error and by deciding if it was “tricky” enough, they had to understand the nature of the error.  I am really excited to see if this process helps students to think more carefully while they solve trig equations and to avoid those common pitfalls.

Day 77: Multiple Representations for Trig Equations

In precalculus, we have begun to look at solving trigonometric equations.  Yesterday, we developed the general rules for finding solutions for the Big Three trig functions: sin^-1x + 2πn, π – sin^-1x + 2πn,  cos^-1x + 2πn, 0 – cos^-1x + 2πn, and  tan^-1x + πn

I am a bit of a stickler as I require students to use the inverse trig function definitions correctly while solving equations.  As an opener, students were asked to do the following:

Find all solutions for the equation: sin2x = – ½.  Now find the particular solutions in the domain: [1,5].  Verify solutions graphically.

My goal for this problem was to connect the algebraic process of solving the equation to the graphical results; that is, I wanted multiple representations and understanding for what was really happening..  Once again I wanted the conceptual underpinning to be solid as my kiddos practiced equation solving procedures; that is, I didn’t want mindless robots solving equations without thinking about what was really happening.

I also got to use my Mathematical Practices labels!  Double score.

Day 74: Snowflake Lane – Trig Style

As one of the Trig Review Stations, student had to graph a trig function alone with it’s reciprocal function.  How boring in and of itself…so decided to have them glue the graph on one side of a pre-cut snowflake (found at Michaels on sale for 99¢) and the initial equation on the other side.  Students used a green pen to graph the initial function and a red pen to graph its reciprocal.  Nice discussions as my students completed the task, particularly one who remarked that this helped him clarify inverse with reciprocal…yay!!

 

Aren’t these fun and also decorates my room for wintertime….notice, no snow yet.  What are ways that you have used a skill practice experience to do double duty as room decoration?

Day 70: Trig Jeopardy

Aren’t Google Searches great! I wanted a quick but engaging way to welcome back my precalc students after our long two week break.  We have a “Big-A Trig Assessment” on Thursday and Friday this week and I wanted a fun way to ease back into the school and trig routine.  I did this search this morning: trigonometry jeopardy powerpoint and found that Ms. McClellen of Charlotteville City Schools had a great powerpoint for reviewing the basics of our Chapter 4 Trigonometry topics; unfortunately, her website wasn’t available so I could give her more and full credit.

I did some tweaking to add in topics that I wanted to review and it was so easy to do!

We had lots of fun reviewing the first day back.

Day 64: Composite Trig Functions

I asked my precalculus students this, “what do you think happens when you add, multiple or compose trigonometric functions with functions from other families? Will the combined functions be periodic?  What type of shape might you expect?”  I had four explorations ready for them to test out conjectures about what happens.  I prefaced the experience by encouraging them to ask “What if? “How?” “Why?” questions as they worked through the explorations…and some actually did.

Initial student comments around the beginnings of the explorations: “It’s a sine function on a slant!” “How are we ever going to find the equation?” “Oh slam…you’re right!”  It was so engaging for me as the teacher listening to the conversations, the conjecturing, and the testing/revising until my kiddos found an equation that actually did what they wanted.  They also looked at predicting what an equation would look like graphed before they graphed it.  Lots of dendrites growing today!

Here is one that combined sine, cosine and tangent.  When asked how each showed up in the final graph, my students were able to point out exactly what they saw and why.

Finally, I had one student on his computer using Desmos with the exploration.  And its available on the iPads for free.  Although I am a big fan of the TI Nspires, I do wonder if Desmos might be a good alternative for some settings.  Have to ruminate on that!

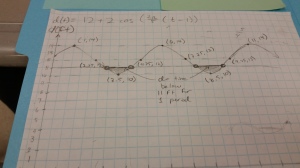
Day 62: Changing Seats using Trigonomety

It is time to change seats!  Usually I have students select a random card and then match with the 3 other people that share the same number.  But I wanted to do the ferris_wheel_card_match as well, and we weren’t going to have time for both.  So I cut out the cards, made sure I had two forms of the equation so that I’d have 4 cards that match in this way: verbal description, graph, 2 equations.  My students had to find their table partners by matching their cards.  Once again, good conversations and questions.

Once they had their new table group, they had to write their names on the seating chart in the correct group.  Worked nicely and we got to do a little bit of the card sort.

How might you use a learning activity to complete a organizational task?

Day 60: Trig Graphs in Under 15 Minutes!

I want my precalculus students to be able to quickly AND accurately graph sinusoidal functions, regardless of the mode, the form or the apparent complexity of the equation.  After all, there are really only up to 5 transformations that can happen to a sinusoidal function: reflection, vertical and/or horizontal dilation, and vertical and/or horizontal translation.  And I want them to be able to clearly and accurately identify the transformed quadrantal points by their coordinates.  Here one of my students chose to color-code the parts of the graph.  The other shows how to determine the horizontal coordinates.  Both of these are done using Notability on the iPad and submitted to Schoology, a learning management system (LMS) our district uses.

I continue to use Foerster’s approach to graphing sinusoidal functions (sometimes referred to as the window method) as I find students have the most success AND understanding.  As part of the development, I want students to create a point-rule and a verbal description of the transformations on the parent function that result in the final graph.  But the practice can be boring and potentially fraught with errors in thinking if students begin graphing in isolation.  So I use complex instruction via a group poster to solidify the process before my students practice on their own.  I have a set of 6 colored, various sided dice in a green-topped container.  Student roll the dice and it determines the equation.  Then they have lots of other things to do once they get the equation.

This year’s students were even more ready to complete these graphs.  I think we did a little more sense-making prior to actually starting to graph and this made it easier for them.  I also used the Online Stopwatch to help them monitor their time.

 

I even had one of my students, who proclaimed early in the year that I had students do way TOO MANY posters, say that he now likes doing posters because they help him understand the ideas better.  Glory be, he made my day!!

What mini-triumphs have you experienced lately?

Day 59: Gettin’ Triggy with Hedbanz

I needed a fun but meaningful way to practice writing equations for sinusoidal functions. I found this idea last year for practicing quadratics, practicing linears and practicing rationals.  I figured I could adapt it for trig functions but I just didn’t have the energy to put it together.  This year I was determined to get it done!

So what is this fabulous activity, you say?  Have you heard of the game, Hedbanz: The Quick Question Game of What Am I? The basic premise for kids try to guess the object that is in their headband based on clues from other players. When I announced that we were going to play Hedbanz, my students were utterly goofy in their excitement.

Initially, I thought I could use Infinite Algebra 2 by Kuta Software to quickly generate graphs.  Unfortunately, I couldn’t control the attributes nor the way graphs were drawn (all horizontal scales were in π forms and max/mins were not easy to determine).  They just didn’t fit what I was looking for; that is, they just weren’t “friendly” enough for this high-paced activity.  I then perused various precalculus books looking for good graphs that students could somewhat readily determine the critical attributes.  I found 32 different graphs, some in radians, some in integer form with clearly determinable extrema.

vs. 

To put together the game, I made the graphs approximately the same size, printed them, cut them out and glued them to different colored 3 x 5 index cards, in groups of 4, although I didn’t end up using the cards as a group activity.  I numbered the cards 1 – 32 on the back of the graphs.  I also found sets of 8 neon colored girls elastic headbands for $1 at our local dollar store, so I bought 5 sets for a total of 40.  I also made a set of answers that I posted at the front of the room for students to self-check.

The kids just loved the activity and the face-to-face discussion was awesome.  I heard things like: “what’s my amplitude/” “what the period?” “what’s the phase shift if I want to write a cosine function? “Hey, the amplitude is NOT the maximum value…you made me get this wrong!”

Sam Shah has the most detailed approach to using this type of activity with your students.

Day 54: Thankful for the Unit Circle

We did a fun activity today in precalculus, reminiscent of an elementary school art activity near Thanksgiving.  We created the hand turkey, but put a trigonometry twist to it.  I gave them this paper to get them started:

Then I said we are making Unit Circle turkey’s for Thanksgiving.  They had to put their thumb on one axis and the pinkie on the other axis.  Then their “feather” fingers became the special angles in the first quadrant.  They added important details, including the angles, the coordinates, etc. along with color.  Interestingly, some students had never made the hand turkey before, but their group partners helped them out and they had fun…even my “curmudgeon” boys who think some of my activities are silly.

 

I was going to have them post their final art work in my room, but they wanted to post in the hall, so we did.