Day 77: Multiple Representations for Trig Equations

In precalculus, we have begun to look at solving trigonometric equations.  Yesterday, we developed the general rules for finding solutions for the Big Three trig functions: sin^-1x + 2πn, π – sin^-1x + 2πn,  cos^-1x + 2πn, 0 – cos^-1x + 2πn, and  tan^-1x + πn

I am a bit of a stickler as I require students to use the inverse trig function definitions correctly while solving equations.  As an opener, students were asked to do the following:

Find all solutions for the equation: sin2x = – ½.  Now find the particular solutions in the domain: [1,5].  Verify solutions graphically.

My goal for this problem was to connect the algebraic process of solving the equation to the graphical results; that is, I wanted multiple representations and understanding for what was really happening..  Once again I wanted the conceptual underpinning to be solid as my kiddos practiced equation solving procedures; that is, I didn’t want mindless robots solving equations without thinking about what was really happening.

I also got to use my Mathematical Practices labels!  Double score.

Day 75: SINning in Stats

Today we begin the journey to Inferential Statistics in my AP Statistics class.  And I use the development of the sampling distribution of a statistic as a means to set up good habits as well as develop the conceptual understanding of why we need to check conditions for the elements of the sampling distribution: Center, Spread, and Shape.

I found that students really struggled with all of the apparently different conditions for the various inference methods we study in second semester.  I really wanted to streamline the process of checking the conditions. After looking at and comparing the various assumptions and conditions, I realized that the two sampling distributions used in the inference procedures about proportions or means boiled down to two things: a random element in the data collection method (simple random sample or randomized experiment), and sample size where one needs both a large enough and a small enough sample to determine the standard deviation and shape.  In addition, I needed to help my students understand the difference between assumptions and conditions.

Here is a summary of what I found:

Assumptions:

Independence Assumption: The sampled values must be independent of each other

The Sample Size Assumption: The sample size, n, must be large enough

Assumptions are hard—often impossible—to check.  Still, we need to check whether the assumptions are reasonable by checking conditions that provide information about the assumptions.  The corresponding conditions to check before using the Normal to model the distribution of sample proportions or means are the Randomization Condition, 10% Condition and the Success-Failure Condition/Large Enough Sample Size Condition.

Conditions you can check:

Randomization Condition: The data must be representative of the population. (That is, it must come from a randomized experiment, or from a simple random sample of the population; the sampling method must be unbiased.)

10% Condition: The sample size, n, must be no larger than 10% of the population.

Success/Failure Condition: The sample size must be large enough so that we can expect at least 10 “successes” and 10 “failures”. That is, np > 10  and nq > 10  OR  Large Enough Sample Condition: If the population is unimodal and symmetric, any size sample is sufficient. Otherwise, a larger sample is needed.

I also wanted it have some kind of cognitive framework to fit these ideas.  How could I combine the ideas into chunks that include the essence of the assumptions and conditions?  Well, Random made its own sense, but Independence and the 10% condition were intertwined, and the approximately Normal shape was tied to having a large enough size sample via success vs fails or simply a larger sample was better.

Acronyms are great memory devices, especially when first learning about something new and complex.  The acronym is a simple organizational tool that reminds the user of the complex ideas.  My next thought was what kind of acronym could I come up with for these?  RIN (for random, independence and normal)..but there was no real hook or interesting connection with RIN.  How about SIN where S stood for random Sample…but that was somewhat suspect because not all inference is about sampling, so I did stretch it a little to say SRS or random assignment (they both sound essy).   And I use the catchy phrase, “It is a SIN to not check the conditions.”  And I have found that my kiddos don’t forget to check them….phewww!

Here is an example of how we talk through these ever important assumptions and conditions.  As the year progresses, we fine-tune and focus in on the important distinctions, but the acronym SIN and these three words give us a simple framework to talk about the distinctions.  To set the groundwork for next semester, I have students recognize the assumptions/conditions AND what the condition guarantees.

 

Day 64: Composite Trig Functions

I asked my precalculus students this, “what do you think happens when you add, multiple or compose trigonometric functions with functions from other families? Will the combined functions be periodic?  What type of shape might you expect?”  I had four explorations ready for them to test out conjectures about what happens.  I prefaced the experience by encouraging them to ask “What if? “How?” “Why?” questions as they worked through the explorations…and some actually did.

Initial student comments around the beginnings of the explorations: “It’s a sine function on a slant!” “How are we ever going to find the equation?” “Oh slam…you’re right!”  It was so engaging for me as the teacher listening to the conversations, the conjecturing, and the testing/revising until my kiddos found an equation that actually did what they wanted.  They also looked at predicting what an equation would look like graphed before they graphed it.  Lots of dendrites growing today!

Here is one that combined sine, cosine and tangent.  When asked how each showed up in the final graph, my students were able to point out exactly what they saw and why.

Finally, I had one student on his computer using Desmos with the exploration.  And its available on the iPads for free.  Although I am a big fan of the TI Nspires, I do wonder if Desmos might be a good alternative for some settings.  Have to ruminate on that!

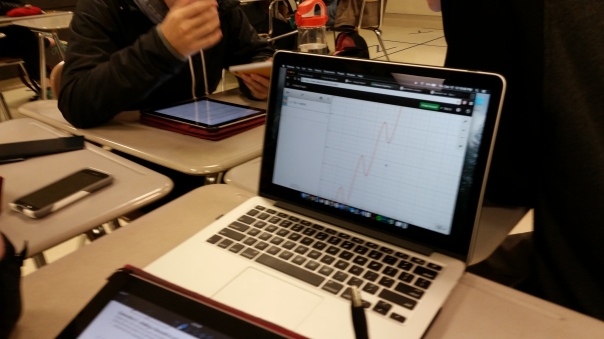
Day 61: The Challenges of Combining Random Variables

In AP Stats, we’ve begun our study of how random variables can be combined.  I use a very simple partner activity to get students thinking about what we can and can’t do when combining random variables.

APS 6.2 – Day 2 Combining Random Variables Partner Activity

Through doing the first part of the activity, I found some students didn’t actually understand that the term “probability distribution” meant to create the table with the random variable, X, and their related probability values.  They were just writing out what the probabilities were.  Also, determining the standard deviation from a probability distribution was still elusive.  So we spent some time reviewing the formula followed by how to use the calculator to make the calculations easier.  (Sorry, forgot to take photos today ;{

I’m worried that my kiddos lost sight of the purpose of the activity in the process of completing the calculations.  We did finish the questions for the combined random variable X + Y; yet I am very sure that the conceptual understanding is missing.  So on block day Wednesday, we’ll revisit the reasons behind the calculation of the standard deviation using a simplified version of  Dave Bock (of Cornell University)’s AP article entitled, Why Variances Add–And Why It Matters.  We’ll talk about his coined phrase “Pythagorean Theorem of Statistics” as well as explore his three questions:

1. Why do we add the variances?
2. Why do we add even when working with the difference of the random variables?
3. Why do the variables have to be independent?

We’ll then look at one of the Math XL homework questions:

followed by having my students look at the work they did for the combined random variable X – Y on the Partner Activity.  Wednesday will be a busy day, and luckily we have 90 minutes to fortify their understanding.  Keeping my fingers crossed.

Day 60: Trig Graphs in Under 15 Minutes!

I want my precalculus students to be able to quickly AND accurately graph sinusoidal functions, regardless of the mode, the form or the apparent complexity of the equation.  After all, there are really only up to 5 transformations that can happen to a sinusoidal function: reflection, vertical and/or horizontal dilation, and vertical and/or horizontal translation.  And I want them to be able to clearly and accurately identify the transformed quadrantal points by their coordinates.  Here one of my students chose to color-code the parts of the graph.  The other shows how to determine the horizontal coordinates.  Both of these are done using Notability on the iPad and submitted to Schoology, a learning management system (LMS) our district uses.

I continue to use Foerster’s approach to graphing sinusoidal functions (sometimes referred to as the window method) as I find students have the most success AND understanding.  As part of the development, I want students to create a point-rule and a verbal description of the transformations on the parent function that result in the final graph.  But the practice can be boring and potentially fraught with errors in thinking if students begin graphing in isolation.  So I use complex instruction via a group poster to solidify the process before my students practice on their own.  I have a set of 6 colored, various sided dice in a green-topped container.  Student roll the dice and it determines the equation.  Then they have lots of other things to do once they get the equation.

This year’s students were even more ready to complete these graphs.  I think we did a little more sense-making prior to actually starting to graph and this made it easier for them.  I also used the Online Stopwatch to help them monitor their time.

 

I even had one of my students, who proclaimed early in the year that I had students do way TOO MANY posters, say that he now likes doing posters because they help him understand the ideas better.  Glory be, he made my day!!

What mini-triumphs have you experienced lately?

Day 50: Definitions Without Words

 

Today I wanted my precalculus students to recap the coffee filter activity.  But how to do it in an interesting way?!  I found a great website site that has some awesome .gif files of mathematical concepts in picture form.  Check it out!! There are some pretty amazing visual depictions of important (or not so important) math ideas.

Here is the one I found for visually communicating the definition of a radian.  Love it!!

So the Opener question I asked was this:

Explain how this .gif demonstrated the definition of a radian.  What is the conversion relationship between radians and degrees?

Also, as an added a reminder of the mathematical practices, I  asked my kiddos which math practices they used to complete their write-up.  Lots of bang for the time allotted!  I think I will continue to use this as a follow-up to the “What in the World is a Radian?” activity.

Day 48: Coffee Filter Radians

This activity has been done in so many ways that I’m not sure I can add anything to the body of knowledge.  Here is a fuller explanation from last year’s “What in the World is a Radian?” activity.

However, based on a workshop I attended at the Northwest Mathematics Conference in Whistler, BC. last month called  Folded Paper and String Graphs of Sinusoidal Functions given by Susan Robinson (Gulf Islands Secondary School, Salt Spring Island, BC), I did a little more with the activity.  Once we had located the whole number radians on the coffee filter and developed the idea of what a radian really was, students readily named the location of π and 2π on their Unit circle.  I used this to leverage the quadrantal angles via folding the filter into quarters.  We labeled the angles using a chosen color.

Then the thinking caps came on!!  They were familiar with the special angles in degree form, so I asked them how we would get 45º angles…and they played right into my hands, saying “fold the quarters in half.” So we did and then discussed what the radian equivalent would be, and they said π/4.  We then counted around the circle and name the other non-quadrantal angles.  They chose a different color and labeled all of these angles on their filter.  We looked at patterns in the values and they came up with “π/4 multiplied with odd numbers.”  We also talked about why we didn’t include the “π/4 multiplied with even numbers.”  You see where this is going, huh?  Sense-making is soooooo FUN!!  We continued for the π/3 and π/6 families of angles.  By the time we got to π/6 angles, they were answering the questions before I asked them.

In reflection, I will continue with this new addition to the activity because I think it was a missing link in year’s past.  I particularly like the idea of color-coding the angle names.

NOTE 11/18:

Today, we took out the coffee filter and then began to talk about the “family of angles” and related trig ratios.  The color-coded angles really brought home the relationship between the angles in the family, the related right triangle and the trig values.  Definitely I will continue to build the Unit circle in this way!!

Day 39: Confused about Fractions

 

Today in precalculus, I was beat over the head about how important it is for students to truly understand the conceptual underpinnings of learned procedures.  I asked students to evaluate a difference quotient expression where the function was the inverse function:

Simplify the expression  when  :   Then evaluate when x = 3 and h = 0.

Did I learn a lot about what students had memorized poorly as well as misconceptions.  What a great opportunity to explore via asking the right questions their misunderstandings as well as give them tools for figuring things out when they are not sure how the mechanics work.

This problem also gave us an opportunity to revisit the idea of an undefined value when it is indeterminant in nature; i.e. 0/0 and how that is related to the point discontinuity.  Good stuff today!

Day 28: What Type of Discontinuity?!

This was a red-letter day in precalculus…at least for the teacher.  As an opening question, I asked my class this simple question:

Is x = 3 the location of an infinite discontinuity or a removable discontinuity?  Explain how you know.

As I was walking into class to set up, I decided to change it up.  I asked the students to answer the question silently and individually.  Then, once everyone had an answer, I asked them to move to one side of the room or the other depending on their answer of vertical asymptote versus removable discontinuity (hole).  Then as a group, they needed to come up with one convincing mathematical reason their choice was correct.  You can see the two huddles below.

 

Then I was the scribe as each group gave a reason.  After each group commented, the other group needed to give a convincing statement to either support their stance OR refute the other group’s statement…thus the different colors.  After each group gave a statement, they had time to re-huddle and/or change sides.  And then we repeated the process.  I was after student voice and academic discourse targeted at each other and not me as the conduit.  They desperately wanted the answer, but I didn’t give it.  So they had to resort to the definitions and theorems to add sophistication and depth to their arguments.

Although this took longer that I had originally planned for the opener (and I had to adjust the subsequent lesson) the end result was that the students, through disciplined discourse, were able to convince themselves of the answer AND had a much deeper understanding of the underlying concepts.  It was so exhilarating to see the metamorphosis of their graph of the ideas behind vertical asymptotes and point discontinuities.  They were so proud, and somewhat surprised that they could actually reason through to the correct answer.  I never did tell them 😛

Day 22: Polynomials Block Activity

We have a block schedule so my other precalculus class went through the foldable and poster today.  I really am enjoying my science room with so much space for these kinds of activities!!