Day 174: A More Beautiful Question

I’d say over the past 10 years, I have been reflecting about and trying to improve my questioning techniques with my students.  It seems to be a common thread in much of my lens as I plan each year, attend PD and read.  I have noticed over the years that my questioning is getting better (although it’s got a long way to go…will I every be a master questioner?!).  I bring this up because over the last year as I became a proficient Twitter user, I saw lots of tweets about teacher and student questions in the classroom and references to blogs about classrooms where math curriculum is explored through student questions.  This was a new twist on questioning that has sparked my interest.

One book (and author) that seems to be referenced often is A More Beautiful Question by Warren Berger.  I decided I wanted find out for myself what the big hoopla was all about!  I added it to my list of books for my summer reading.  I ordered it and some others through Amazon and it came yesterday!  Excitement!!  I began to read just the beginning and I ended up reading two chapters.  And I need you to know that I don’t have that kind of time right now to be reading that much, but I just couldn’t put it down.

Here are some quotes I’ve already jotted down:

p.8 by Warren Berger giving the definition:

A beautiful question is an ambitious yet actionable question that can begin to shift the way we perceive or think about something – and that might serve as a catalyst to bring about change.

p. 16 by Stuart Firestein on the potential of a good question:

One good question can give rise to several layers of answers, can inspire decades-long searches for solutions, can generate whole new fields of inquiry, and can prompt changes in entrenched thinking.  Answers, on the other hand, often end the process.

p. 23 by Tony Wagner, a Harvard education expert and Paul Bottino, a Harvard innovation expert on “expertise”:

Known answers are everywhere, and easily accessible.  The value of explicit information is dropping…the real value is in “what you do with that knowledge, in pursuit of a query.”

p. 18 by Stuart Firestein on questioning:

Questioning is a very sophisticated, high-level form of thinking.

And this particular quote got me wondering, if I value questioning and want my students to know that I value it, I must assess it.  Which led to me asking, How can I assess a “good” question?  What are the components of a “good” question?  How can I help my students grow their ability to ask those “good” questions?

What are some books you are planning to read this summer?  What is motivating your choices?  How do you anticipate using the gained knowledge in your practice?

Day 147: It’s That Time of the Year

There is always a pinnacle moment during the second semester when I begin to think, “what do I need to change for next year?!”  And today is that day.  I won’t say that I’m frustrated by my students, but I begin to long for the “start over” free-ness of the beginning of a new year.  I think that’s why I’ve enjoyed my time as a teacher.  I’m an eternal optimist: “It will be better next year,” “I’ll plan so I won’t spend so much time after school every day grading,” “I know I can re-write this unit to be more engaging!” “There’s got to be a better way to do this, and I’ll figure it out this summer.”

So I started my “Beginning of Year ’15” folder.  I have been doing these folders for upwards of 18 years; it is really interesting to look back at how my focus has changed and how some things are central to who I am as an educator.  I guess I have always been a reflective teacher, even before it was “in vogue.” 

So what do I include, you ask.  Here is look at the folder from a year ago:

LEFT SIDE:  Based on the previous year’s PD, reading and conferences, I subconsciously begin to develop a Focus for the year (which eventually develops into a Theme or Saying).  Around this focus, I try to write goals for my students, their parents and myself (both professional and personal).  I then narrow down and hone in on some key things I want to try, I want to change, and I want to keep.

RIGHT SIDE:  This is reserved for technology implementation, specific procedures and student engagement or anything else I want to weave into my whole class experience.

 

So this year, I haven’t actually started to coalesce my thoughts, but I have begun to “gather”. In talking with one of my colleagues, we are interested in working on integrating the Growth Mind Set language and attitudes with our students.  This means some more reading over the summer as well as reflecting and conversing with my co-worker about how we might actually weave this theory into our practice in a seamless way.  I also have added some quick sticky notes.  I will eventually put in a clean sheet labeled for each course with specific ideas to incorporate or replace practices in that class.

 

Day 62: Thankful Times

Today was assessment day just before Thanksgiving Break.  I hate to have assessments on the day before a break, but in AP Stats, the kids actually voted to move the test to Wednesday and they promised to show up…which they did!  I am so thankful for these kids ‘cuz they are honorable and interested young people.  This test was on probability and it seems they either “get it” or they don’t.  I may have to consider a test re-take option based on the standards of the chapter and the AP curriculum, but I need to ruminate on it for a day or two.  Students are doing homework and most of the class notes, but I think some students aren’t using them to make sure they really understand the material.  This may be because they don’t know how to use homework as a tool for deep and authentic learning, so I’ll need to consider how to develop this important and leveraging study skill with seniors who think they know it all (tongue in cheek and smile on my face).

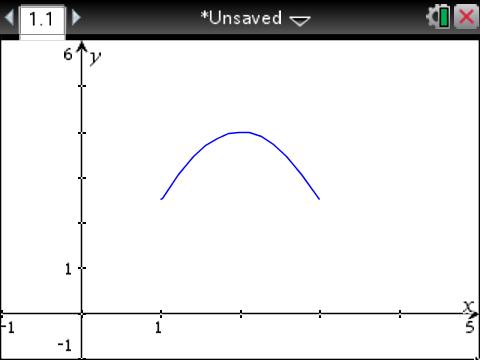
In precalculus there was a quiz after a discussion around the opener:  Given the portion of a sinusoidal function at the right, state its critical attributes, and then write its equation in terms of cosine and sine.

Unfortunately we had slightly shorter periods due to early release, so timing was an issue in one of my classes.  They did a really nice job on the quiz, even on this cool question:  Find the average rate of change between the two points on f(x)= sin(x).

A few were confused about what the “average rate of change” was asking (but this is critical for next year’s experience in Calculus) and small number of others forgot what the output of the function f(x) = sin(x) is the ratio for the input angle, but overall the rest of the kiddos nailed this problem “even though they had not seen one like this before.”  After the quiz, they asked and were smacking their foreheads knowing they “should have known that.”

I truly believe it is critically important for kids to actually transfer learning in unfamiliar settings…and I preach it daily.   I almost always ask a question that they “haven’t seen before” but uses only those concepts and processes they have practiced a great deal.  I tell them that I can’t ask them anything that they don’t have the tools to approach and find an answer, but they may have to use their knowledge in a new way which requires them to really understand the concepts underlying the process they are learning. And they are beginning to embrace the expectation.  I am so thankful for that willingness to stretch and learn and retain that my precalculus students are growing into this year!

Happy Thanksgiving!  What are you thankful for this year?

Day -4: CCSS Practice and Practices

Worked with my course partner to develop an introduction to the 8 Math Practices in our precalculus course for the first week of school.  We’re using the task as a way to get the kids talking about the practices (we’ll do some problem-solving activities in the 2nd week of the course with the practices) while introducing them to group work responsibilities using the Complex Instruction model.  With the poster*, I wanted to plant the seed regarding the difference between math practice and math practices; math practice is about developing skills whereas math practices is about mathematical habits of mind. Any-hoo, here it is:

Task: The 8 Mathematical Practices

This task is about thinking and doing work like a mathematician!  The goal is to become familiar with the eight mathematical practices.

• Resource Manager:  Find and hand out the Math Practices foldable.  Make sure each person in the group cuts out and folds the Math Practices foldable correctly.
• Facilitator:  Assign one member to teach two of the eight practices from the foldable.  Discuss what each might mean in Honors Precalculus.  You might also search “Common Core Mathematical Practices” with your iPad for additional details about them.
• Team Captain:  Once the group has shared what the 8 practices are, have each member rate their ability to do each practice using Fist to 5:  fist = can’t do this practice….5 = superstar at this practice.  Find the average for each practice.
• Recorder/Reporter:  Have each person write down their personal rating next to the practice in their packet.  Record the group average for each practice in the assigned location.  Look around the room to find it.

*I’ve looked through so many sites, and I can’t find where I originally got the poster pictured above….I want to give credit where credit is due, so if the poster is yours, PLEASE let me know so I can give you credit!!