Day 85: Polar Equations Finished!

They are done!  The polar equation graphs my precalc students started on Friday are finished…in fact they came into class asking if they could have time to finish ‘cuz they really wanted to see the final results.  I like the component of finding the name of their equation type as well as researching then sharing least 2-3 interesting facts about their polar equation.

Day 84: Hands on Polar Equations

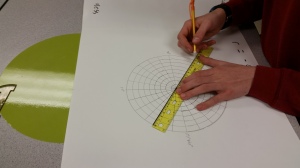
Many years ago (I don’t want to say how many but it was before we had access to graphing calculators), I had my students hand draw various polar equations.  Having technology so readily available now, this project had been shelved and collecting dust. I decided today that I wanted my precalculus students do experience a tactile activity today.  Although I love polar equations, it just didn’t fit the timeline this semester (maybe we’ll revisit next semester).  But why not give them an initial exposure to Polar Equations and their graphs as a way to review polar coordinates just before finals…and besides, the graphs are fun and unexpected.

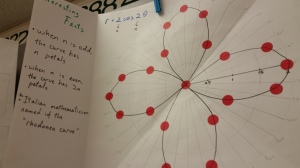
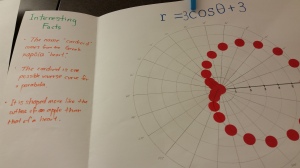
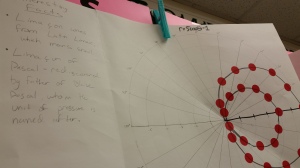
I wrote up the activity and made some decisions about how to have students make posters.  A few years ago our department invested in large boxes of poster paper (you can see the poster paper in many of my posts) which was a pretty cheap investment for the amount of paper…and the box seems to last for a couple of years at least.  I wanted the paper to be a square in order to find the center and create the polar graph paper.  Once I folded to create the square, I thought, why not use the flap for added info.  Here is my prototype that I had posted on the front white board.

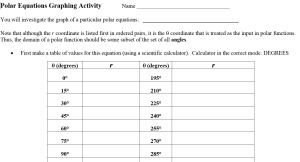
I then wrote up the directions, including a chart for my students to record the r-values for their equation. I did not tell them the names of the graphs, just handed out various equations; each student got a unique one. I was ambitious with what I wanted them to do afterwards (and we didn’t get that far), but I would keep the “interesting facts” part of the activity.

Then I handed out the directions and away they went.  I had hoped they would finish in the class period, but some of my students are very meticulous so it took a while for them to create the polar graph paper on the poster.  I am still pondering how to improve that aspect of the activity.  Anyway, here are some photos of the activity in progress:

 

  

Hopefully they will finish on Monday.  Happy Week-end

Day 136: Do The Really Intersect?

Its the day before Spring Break.  We finished the Midterm yesterday and they did brilliantly!  Not a great time to introduce new material.  An easy way out is to “show a movie” but to waste precious time with students with an experience that has no real academic purpose goes against everything I believe.

So, how do I keep my precalculus students engaged and interested?  I wanted something that reviewed an old, but not critical, learning but added an intellectual twist that will catch and keep their attention.  And I remembered a workshop I attended about 5 years ago (I’m sorry but I just can’t find the name of who presented and would love to give you credit…just comment below with your name and any other info you’d like to share) using the Nspire to look at the relationship between polar and rectangular equations in graph form.  The presenter shared 3 Nspire documents that had nice animations.

For this experience, though, I used Geogebra because the kids could manipulate easily with their iPads.

It was the 4th document which inspired me to create an investigation around a system of two polar equations.  Luckily the document was created, but I wanted my students to reflect more while using the Nspire document.

 

For instance, I had the students do this:

Move to 2.1. Without talking to your group, watch the animation alone!  You must watch carefully because you cannot re-graph again.  Try to observe how many times these graphs’ paths intersect.

1. What did YOU notice?
2. Once everyone has completed the task alone, talk with your group. What did other people in your group notice? Try to paraphrase your discussion.

Then later the real thinking started.  My students  used their Nspire to do the following:

Move to 4.1. You will see the results of graphing the two polar graphs in the rectangular plane.  Does this affect your answer?  Be specific!

1. Use the rectangular graphs to give the coordinates of the points (in polar form please) of intersection of the limacon, r₁ = 3 + 2 cosθ, and the four-leaved rose, r₂ = 5 sin(2θ). Label the intersection points on both the rectangular graph and the polar graph.  The first point is labeled P₁ on both graphs.

1. Why could the apparent intersection point Q₁ be called a “false” intersection point? What aspect(s) of a polar graph make it appear to be a point of intersection?  Label the other false intersection points on the polar graphs in the same manner.
2. Show on the rectangular graphs above that the second-quadrant angle θ for point Q₁ corresponds to a point on the limacon but not to a point on the rose. What are the coordinates of point on the rose that correspond to the location Q₁?  Is there a mathematical relationship between the point on the limacon related and the point on the rose which correspond to the location Q₁?

I was so delighted with how engaged my students were…to see their heads down, fingers posed over their iPads and some conversations, too.  The Math Practices were everywhere today! In fact, they didn’t even realize class was over, and that’s a biggie for a 7th period just before Spring Break.

Happy Spring Break!  Happy Easter!  I’ll be back in a week.

Day 84: Cool Polar Graphs

Today in Precalculus, my students finished their exploration of polar graphs.  One of the nice things about the Nspire is the color aspect: each relationship is graphed with a different color.  Here a student was looking at the equation: r²=a²·cos(2θ).  Although it is hard to see, they were trying different values for a and exploring how to graph when the equation needs to be in the form r(θ) not r².  Great discussions!

After students finished yesterday’s exploration today, I gave them a graph and asked if they could figure out the equation I used to get the graph.  I asked them to see what would happen when they try equations different than the one’s they had already explored.  This led to other types of graph.  Below is one of the graphs they tried to get the one I had given (not the same one).  Thinking ahead, this could be a great lead in to comparing the rectangular equation to the polar equation.

 

Day 83: Polar Graph Exploration

Today my precalculus kids began a Polar Graphs exploration.  It was a great way to have them use polar coordinates again while also letting them see some spectacular graphs.  Since it is an exploration, the gist is to look for patterns, and polar graphs lend themselves easily to pattern posing, pattern checking and revising, and pattern generalization.

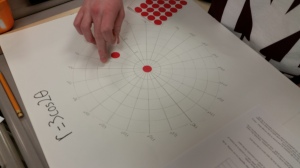
In the past I have given students students a card with a polar graph equation, a large polar grid and a sheet of mini dots.  They evaluate the equation for lots and lots of angle values, determine the related r-values and then “graph” the point with the mini dots.  Different than using the calculator but more time consuming and the students get less exposure to the variety of polar graphs and less opportunity to sense-make with their peers….but I did have some nice examples to put on my wall.

I am thinking if we have time to revisit polar graphs, I’d like to use this idea in conjunction with the related rectangular trig graph to develop an understanding of the relationship between the two.  How do you connect (or re-connect) old ideas with new ones?